Solution Exercise 2
On the spreadsheet sheet “DTS RAW”, the temperature values of the calibration baths have been inserted for the time 4:28 hours, along with the calculated average Stokes and anti-Stokes signals from the sections of the fiber in each of the calibration baths. The “A” matrix for the calibration equation has also been populated for the 4:28 hours. Begin the process of calibration by taking the matric inverse of A using the Excel matrix inversion function “MINVERSE”. Next, the “b” matrix has already been populated for you with the product of the bath temperaturs and the ratio of the log of Stokes and anti-Stokes power from time = 4:28 hours. Finally, calculate the calibration parameters by making the matrix multiplication of A-1 * b using the Excel function MMULT . The resulting calibration parameter should be:
Time = 4:28 hours
γ = 484.28 K
C = 1.29 (dimensionless)
Δα = 8.866×10−5 m−1
Shown below ore the measured stream temperatures at 4:28 (in blue) as compared to the calibrated ones using the calibration coefficients from part a and the calibration equation. To calculate the calibrated temperatures, you can copy the calibration equation over from time = 3:10 PM (column. F in DTS RAW sheet) and past into and paste into column L, being sure to adjust the cell calls to call the DTS data from 4:28 hours. Overall, the calibration reduced the stream temperatures by a relatively similar amount, suggesting that the presumed differential attenuation coefficient was close to the correct value, i.e., there was little slope change in the results as shown in the figure below.
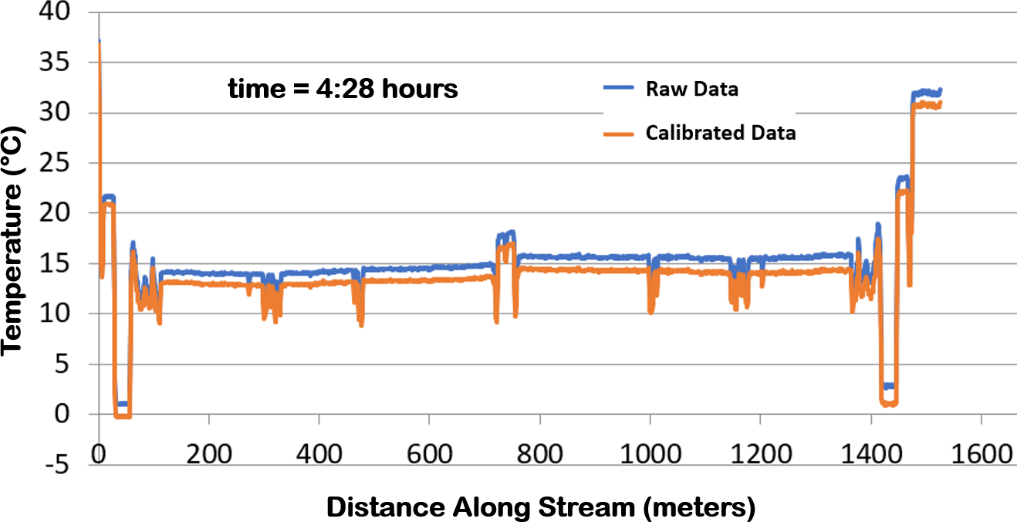
Raw and calibrated data for 4:28 hours trace.
First calculate the Root Mean Squared Error (RMSE) from each 10 m length of fiber in each of the calibration baths used in the calibration. The RMSE is calculated as shown below:
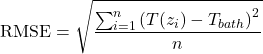 |
where:
| T(zi) | = | calibrated temperature at each point on the calibration section, in this case from 9.68 m to 25.9 m for Bath 1 (including 17 measurements), from 30.99 m to 55.34 m for Bath 2 (including 25 measurements) and from 724.99 m to 736.13 m for Bath 3 (including 24 measurements) |
| Tbath | = | assumed “true” temperature of the bath as measured by the independent temperature sensor |
| n | = | number of observations (in this case 17 points for Bath 1, 25 points for bath 2 and 24 points for Bath 3) |
The calculated temperatures from both traces within the two calibrations baths, and the corresponding measured bath temperatures are shown in the table below.
Data from two DTS traces within calibration baths. Calibration Bath 1 begins at 9.688 m and ends at 25.92 m. Calibration Bath 2 begins at 30.994 m and ends at 55.344 m. Calibration Bath 3 begins 724.99 m and ends at 736.13 m. Transitions between Baths are indicated by shading.
| Time = 15:10 | Time = 4:28 | |||||
| Cable distance (m) | Tcalibrated | Tbath | Cable distance (m) | Tcalibrated | Tbath | |
| 9.688 | 19.20064958 | 19.17 | 9.688 | 20.84919341 | 20.89 | |
| 10.702 | 19.02876606 | 19.17 | 10.702 | 20.86304149 | 20.89 | |
| 11.717 | 19.12327031 | 19.17 | 11.717 | 20.85627611 | 20.89 | |
| 12.731 | 19.13207407 | 19.17 | 12.731 | 20.9300866 | 20.89 | |
| 13.746 | 19.15839026 | 19.17 | 13.746 | 20.92466545 | 20.89 | |
| 14.761 | 19.20355003 | 19.17 | 14.761 | 20.9146521 | 20.89 | |
| 15.775 | 19.26246247 | 19.17 | 15.775 | 20.91940108 | 20.89 | |
| 16.79 | 19.2119609 | 19.17 | 16.79 | 20.85922323 | 20.89 | |
| 17.804 | 19.18031936 | 19.17 | 17.804 | 20.90630153 | 20.89 | |
| 18.819 | 19.1534668 | 19.17 | 18.819 | 20.89528913 | 20.89 | |
| 19.834 | 19.23392457 | 19.17 | 19.834 | 20.96513629 | 20.89 | |
| 20.848 | 19.18208139 | 19.17 | 20.848 | 20.87671062 | 20.89 | |
| 21.863 | 19.10911496 | 19.17 | 21.863 | 20.84182784 | 20.89 | |
| 22.877 | 19.23165354 | 19.17 | 22.877 | 20.94894786 | 20.89 | |
| 23.892 | 19.15091432 | 19.17 | 23.892 | 20.81938265 | 20.89 | |
| 24.907 | 19.14782634 | 19.17 | 24.907 | 20.8582565 | 20.89 | |
| 25.921 | 19.18368123 | 19.17 | 25.921 | 20.90557791 | 20.89 | |
| 30.994 | 0.148849032 | -0.17 | 30.994 | 0.048998697 | -0.17 | |
| 32.009 | -0.150060865 | -0.17 | 32.009 | -0.094790973 | -0.17 | |
| 33.023 | -0.170548613 | -0.17 | 33.023 | -0.245489913 | -0.17 | |
| 34.038 | -0.217096836 | -0.17 | 34.038 | -0.17536847 | -0.17 | |
| 35.053 | -0.249312361 | -0.17 | 35.053 | -0.276940387 | -0.17 | |
| 36.067 | -0.185950565 | -0.17 | 36.067 | -0.218028531 | -0.17 | |
| 37.082 | -0.18260034 | -0.17 | 37.082 | -0.230442845 | -0.17 | |
| 38.096 | -0.2037029 | -0.17 | 38.096 | -0.226951929 | -0.17 | |
| 39.111 | -0.148092379 | -0.17 | 39.111 | -0.128530218 | -0.17 | |
| 40.126 | -0.188837919 | -0.17 | 40.126 | -0.189548408 | -0.17 | |
| 41.14 | -0.22549814 | -0.17 | 41.14 | -0.288113919 | -0.17 | |
| 42.155 | -0.193666694 | -0.17 | 42.155 | -0.250570457 | -0.17 | |
| 43.169 | -0.197713762 | -0.17 | 43.169 | -0.184649281 | -0.17 | |
| 44.184 | -0.210577254 | -0.17 | 44.184 | -0.147120206 | -0.17 | |
| 45.199 | -0.211584209 | -0.17 | 45.199 | -0.166080062 | -0.17 | |
| 46.213 | -0.199698358 | -0.17 | 46.213 | -0.168688627 | -0.17 | |
| 47.228 | -0.248931213 | -0.17 | 47.228 | -0.252037261 | -0.17 | |
| 48.242 | -0.162753158 | -0.17 | 48.242 | -0.138284041 | -0.17 | |
| 49.257 | -0.226487371 | -0.17 | 49.257 | -0.147730613 | -0.17 | |
| 50.271 | -0.19886561 | -0.17 | 50.271 | -0.182657969 | -0.17 | |
| 51.286 | -0.191672478 | -0.17 | 51.286 | -0.249715167 | -0.17 | |
| 52.301 | -0.192145245 | -0.17 | 52.301 | -0.181643111 | -0.17 | |
| 53.315 | -0.228227478 | -0.17 | 53.315 | -0.132198188 | -0.17 | |
| 54.33 | -0.135567442 | -0.17 | 54.33 | -0.158077101 | -0.17 | |
| 55.344 | -0.196743244 | -0.17 | 55.344 | -0.20379568 | -0.17 | |
| 724.977 | 14.68213985 | 14.637 | 724.977 | 16.35891506 | 16.57 | |
| 725.992 | 14.57358998 | 14.637 | 725.992 | 16.51709393 | 16.57 | |
| 727.006 | 14.68397197 | 14.637 | 727.006 | 16.58589748 | 16.57 | |
| 728.021 | 14.63061624 | 14.637 | 728.021 | 16.60245739 | 16.57 | |
| 729.035 | 14.55845899 | 14.637 | 729.035 | 16.54309278 | 16.57 | |
| 730.05 | 14.5785534 | 14.637 | 730.05 | 16.44268414 | 16.57 | |
| 731.065 | 14.63127404 | 14.637 | 731.065 | 16.56721847 | 16.57 | |
| 732.079 | 14.64882637 | 14.637 | 732.079 | 16.70140054 | 16.57 | |
| 733.094 | 14.54051841 | 14.637 | 733.094 | 16.61988398 | 16.57 | |
| 734.108 | 14.65651409 | 14.637 | 734.108 | 16.49448137 | 16.57 | |
| 735.123 | 14.71285461 | 14.637 | 735.123 | 16.56808195 | 16.57 | |
| 736.138 | 15.08866249 | 14.637 | 736.138 | 16.02728215 | 16.57 | |
| 724.977 | 14.68213985 | 14.637 | 724.977 | 15.34916677 | 16.57 | |
| 725.992 | 14.57358998 | 14.637 | 725.992 | 15.17789982 | 16.57 | |
| 727.006 | 14.68397197 | 14.637 | 727.006 | 16.35891506 | 16.57 | |
| 728.021 | 14.63061624 | 14.637 | 728.021 | 16.51709393 | 16.57 | |
| 729.035 | 14.55845899 | 14.637 | 729.035 | 16.58589748 | 16.57 | |
| 730.05 | 14.5785534 | 14.637 | 730.05 | 16.60245739 | 16.57 | |
| 731.065 | 14.63127404 | 14.637 | 731.065 | 16.54309278 | 16.57 | |
| 732.079 | 14.64882637 | 14.637 | 732.079 | 16.44268414 | 16.57 | |
| 733.094 | 14.54051841 | 14.637 | 733.094 | 16.56721847 | 16.57 | |
| 734.108 | 14.65651409 | 14.637 | 734.108 | 16.70140054 | 16.57 | |
| 735.123 | 14.71285461 | 14.637 | 735.123 | 16.6198398 | 16.57 | |
| 736.138 | 15.08866249 | 14.637 | 736.138 | 16.49448137 | 16.57 | |
The RMSE calculated using the equation above and the temperatures shown in the table above for each bath is 0.053 and 0.074 °C for the first two baths at the 15:10 time slice. The RMSE is 0.14 °C, for the bath at the far end of the cable (Bath 3), approximately twice that of the baths at the beginning of the cable and is a result of few photons being returned from the distant end of the cable, and therefore more noise in the returned signal.
For the 4:28 time slice, the RMSEs for the baths near the start of the cable are similar (0.039 and 0.069 °C) to the previous time and consistent with expectations. However, the RMSE for the far calibration bath during the nighttime trace is 0.40 °C; much higher, and suggests that the cable loop in the stream was not at a uniform temperature. Most of the RMSE is derived from one measurement in the middle of the calibration coil which is ~1 °C colder than all the rest of the measurements. Likely reasons may be that this portion of the cable was not in good contact with the stream or may have been partially exposed above the water surface during the night time due to a change in river stage or other disturbance. These data point out the value of looking closely at all of the data and investigating anomalous readings.
