4.3 Fractionation and Enrichment Factors
To quantify the fractionation of isotopes between two phases or compounds, the fractionation factor, , is used as shown in Equation 3.
|
|
[latex]\alpha=\frac{R_{\text {reactant }}}{R_{\text {product }}}[/latex] |
|
where:
|
R |
= |
isotope ratio, such as 2H/1H (dimensionless) |
For example, as expressed by Equation 4.
|
|
𝛼2𝐻 (𝑤𝑎𝑡𝑒𝑟−𝑣𝑎𝑝𝑜𝑟) = (2H/1H)water |
|
This factor describes the partitioning of an isotope between two phases or compounds, which is determined by the temperature, chemical bonds and other atomic scale properties of the element. Importantly, the fractionation factor is temperature dependent; in other words, at equilibrium, the isotope ratios in the reactant and product vary with temperature (Figure 7), as was first outlined by Urey (1947). Chacko and others (2001) provide more recent and detailed information on fractionation factors and their calculation.
Calculating the fractionation factor for a given temperature is usually done experimentally with enough measurements at different temperatures to develop an equation such as Equation 5.
|
|
𝑙𝑛 𝛼𝑋−𝑌= 𝑎𝑇−2 + 𝑏𝑇−1 + 𝑐 |
|
where:
|
αX–Y |
= |
fractionation factor for transition from X to Y (dimensionless) |
|
X |
= |
subscript indicating reactant compound or state |
|
Y |
= |
subscript indicating product compound or state |
|
T |
= |
temperature (K) |
|
a, b, c |
= |
fitting constants (K2, K, dimensionless, respectively) |
For most isotopic reactions, the fractionation factor, α, is close to 1, meaning ln(α) will be close to 0. If this is multiplied by 1000, then permil units are obtained. δ values are given in permil units. As long as α is indeed near 1, an enrichment factor (ε) can be calculated (Figure 8). The enrichment factor expresses the difference in δ values between reactants and products (Clark, 2015), as shown in Equation 6.
|
|
𝜀 = 1000(𝛼−1) ≈ 1000𝑙𝑛(𝛼) |
|
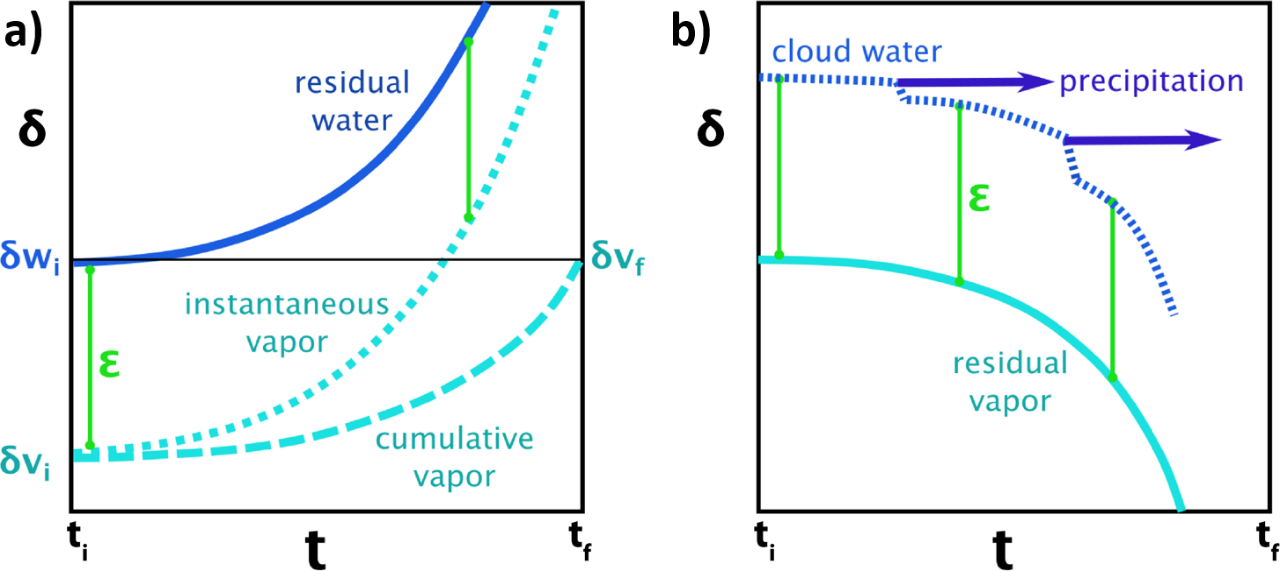
Figure 8 – Graph a) shows the isotopic evolution of a body of water evaporating to vapor over time, at a set temperature and under equilibrium conditions. In this case, the enrichment factor remains constant as the remaining water and the instantaneous vapor evolve. Also, eventually the final total vapor body, assuming no losses from the system, has the same isotope composition as the initial water body. Graph b) shows the isotopic evolution of vapor, cloud and precipitation, for constant temperature and equilibrium condensation.
Importantly the variation in equilibrium fractionation factors is systematic, because lower temperatures always result in higher fractionation factors and vice versa. This temperature dependence is the fact enabling paleoclimate work. The isotopic composition of a material, such as ice in a glacier, depends on the temperature at which the snow or ice crystallized. Calcite in a speleothem can also be used, as the calcite crystallization occurs at a given temperature in the presence of groundwater, which once was precipitation. With enough measurements to establish an accurate average, the isotopic composition of the original precipitation will be known, and if an age can be calculated for the glacier or speleothem, then the temperature at a specific time and place can be reconstructed.
