4.4 Rayleigh Distillation

Around the turn of the 20^th century, Lord Rayleigh proposed a law to describe the changing composition of an original pool of mixed liquids as it is progressively distilled (Lord Rayleigh, 1902). This law relied on the fact that the differential rate of evaporation of the two liquids is known. This was before stable isotopes had been discovered, but it turns out to perfectly predict the theoretical rate at which a reservoir of water will change isotope composition as it loses water to another reservoir through evaporation, freezing, etcetera. The equation Rayleigh proposed is show here as Equation 7 (Clark, 2015).

where:

If an imaginary block of moisture laden atmosphere (a vapor body) has water removed by condensation to form a cloud, there will be an isotopic difference between the vapor and cloud exactly equivalent to the equilibrium fractionation factor, for both H and O isotopes. However, this only holds for the first batch of condensation, because the remaining vapor will immediately change its isotope composition due to the fractionation factor causing heavier isotopes to preferentially condense into cloud droplets. This leaves the vapor body isotopically lighter, which means future condensate will be lighter (Figure 8).

If we envision someone fishing tries to catch the biggest fish in the sea, even though she consistently catches fish that are 1 kg heavier than the average weight of all the fish (the fractionation factor), then as those fish are removed, the average weight of fish in the sea decreases, and so will the weight of each fish in her catch. Sadly, this analogy for Rayleigh distillation is also the true story of fish in the oceans over the last century or so.

Rayleigh distillation is applicable to equilibrium situations, such as cloud formation, where vapor and cloud droplets are in contact long enough for equilibrium fractionation to apply. In settings with orographically driven rainout in a high precipitation location such as the Azores in the north Atlantic which receives 1500 mm/a (Antunes et al., 2019) or for heavy frontal precipitation in California (Mix et al., 2019), Rayleigh distillation gives a reasonable approximation of the stable isotope behavior. In higher latitudes and deeper continental locations, for example the Canadian Rockies (Figure 9), an orographically adjusted Rayleigh model is better for predicting isotope composition of precipitation than a linear Rayleigh distillation (Sinclair et al., 2011).

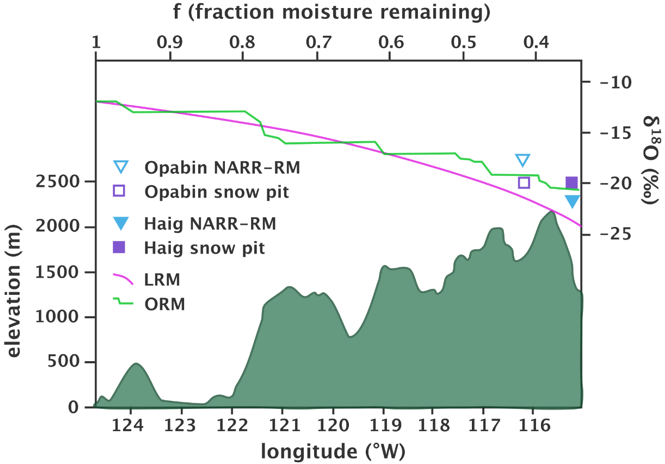
Figure 9 – Regional investigation of the applicability of Rayleigh distillation models to predict stable isotope content of precipitation. This study used three models to predict the stable isotope composition of snowfall in the Canadian Rockies, at two sites, the Opabin and Haig Glaciers. Actual measurements from snow pits are precipitation weighted means. The three models are the NARR-RM (North American Regional Reanalysis – Rayleigh model), the LRM (linear Rayleigh model) and the ORM (orographic Rayleigh model). The ORM can be seen to produce values closest to the actual precipitation seen in the snow pits (after Sinclair et al., 2011).

For a fractionating process, such as a chemical reaction or diffusion in a porous medium like an aquifer, Rayleigh distillation overestimates the changes to the original reservoir, or the reactants. This is due to the rate limiting effects of transport through the aquifer matrix or kinetic reaction effects. Use of a lower fractionation factor partly resolves this problem, but calculation of this lower fractionation factor is complex (Druhan and Maher, 2017).