2.3 Sources of In-Situ Stress and Differential Stress‌

The in-situ state of stress in a rock mass is generally the sum of the gravitational and tectonic stress components (e.g., Zang & Stephansson, 2009). The former is derived from the weight of the overlying rock mass at a given depth. The so-called lithostatic stress is the reference state that results solely from the gravitational component. The tectonic stress component, may partly result from remnant stresses due to paleotectonic events, but the dominant component is the active tectonic stress due to present-day deformation of the Earth’s crust. The origin of the active tectonic stresses at a given location can be derived from first-, second-, and third-order factors (Zoback et al., 1989; Heidbach et al., 2007). The relative displacement of tectonic plates is a first-order stress factor; it is of global scale. The bending of plates and isostatic compensation that lead to erosion and deposition processes (Zoback et al., 1989) are second-order factors (regional scale). Fault-scale stresses are a third-order factor lying between regional and local scale (Heidbach et al., 2007). Apart from gravity, only the tectonic stresses can reach a regional significance. Other stress components have large standard deviations in orientation and magnitude (Zang et al., 2009). One example is the effect of the Earth’s topography near the surface. In mountainous regions, the presence of a number of nearby steep slopes can cause notably variable in-situ stresses; examples of this condition are provided in Section 4.2.

Stresses are more commonly anisotropic than isotropic and vary with orientation (Figure 13 a,b). The stress field can be described by an ellipsoid whose axes, perpendicular to each other, represent the minimum (σ₃), intermediate (σ₂) and maximum (σ₁) principal stresses (Figure 13c). These stresses act in planes orthogonal to each other, and the shear stress on these planes is zero. Figure 13a represents the lithostatic reference state, in which the stresses are derived solely from the gravitational component; this defines a stable condition, that is, the differential stress (σ₁ − σ₃) is not large enough to produce deformation. The differential stress necessary to generate fractures must exceed a certain magnitude, which in general can be met when there is a tectonic component (Figure 13b), as discussed in Section 2.4. However, existing fluid pressures that give rise to the so-called effective stresses may lead to the generation of fractures in situations where the differential stress alone is not large enough to cause the formation of fractures; this is explained in Section 2.5.

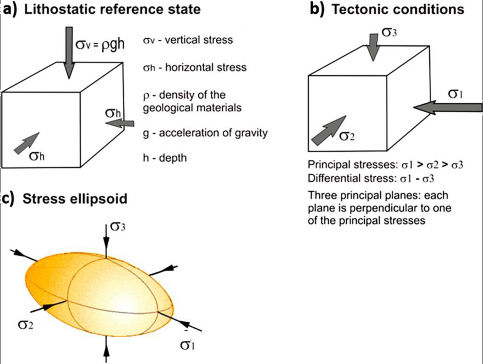
Figure 13 – Subsurface stress. a) In the lithostatic reference state, the vertical stress (σ_v) is the weight of the rock column and the horizontal stress (σ_h) is equal to fraction of the σ_v; its magnitude depends on the mechanical properties of the rock. b) Under tectonic conditions, the three orthogonal stresses are called principal stresses, in which σ₁ is the maximum principal stress, σ₂ the intermediate principal stress, and σ₃ the minimum principal stress. They act on three orthogonal planes that have no shear stress. Failure takes place when the differential stress exceeds a certain value. c) The stress ellipsoid is a three-dimensional representation of the stress vectors acting on all planes within the rock.