Solution to Exercise 3

William W. Woessner

Solution to Exercise 3

3) An exchange study of a pond was conducted by installing three seepage meters (A, B, C) and three adjacent mini-piezometers (small black open circles) as shown in Figure Exercise 3. Using the data provided compute the following:

a) The vertical hydraulic conductivity of the bed sediments at location A.

b) The VHG for B.

c) The seepage flux for C.

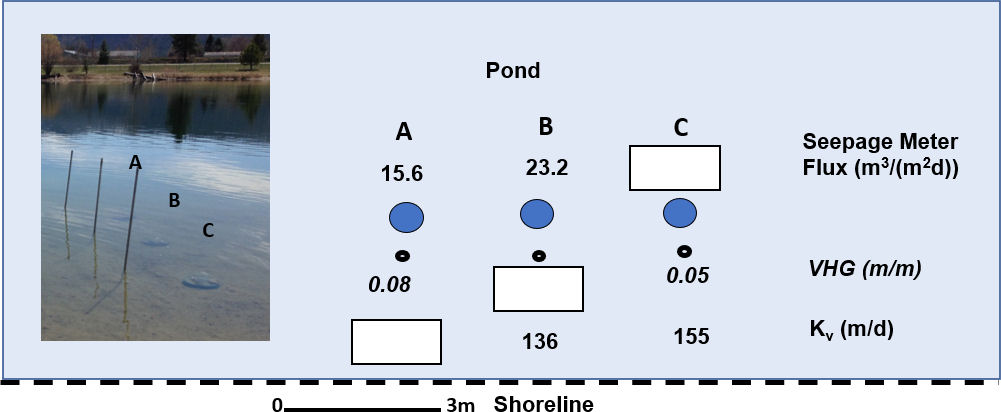
Figure showing an exchange study at a pond constructed in a sand and gravel aquifer — **Figure Exercise 3 –** An exchange study at a pond constructed in a sand and gravel aquifer. Three seepage meters, A, B and C (blue drums in the picture and blue circles in the map view), were installed about three meters from the shoreline. Adjacent to the meters, mini-piezometers (vertical tubes in the picture and black open circles in the map) were driven about 15 cm into the sand and gravel sediments of the bed. Seepage rates, VHG, and estimates of the bed vertical hydraulic conductivity were obtained for each of the three seepage meter locations (Woessner, 2020).

SOLUTION:

The seepage meters directly measure groundwater seepage, flux (q). Using Darcy’s law, the relation among seepage, vertical gradient and vertical hydraulic conductivity is as follows:

q = Q/A = –K_v Δh/ΔL_v = -K_v(VHG)

where:

K_v is the vertical hydraulic conductivity (L/T)

Δh is the change in head in the direction of groundwater flow, lowest head minus the highest head, in this case (pond surface elevation) – (groundwater elevation) (L)

ΔL_v is the difference between the pond bottom and the open end of the mini-piezometer (L)

VHG is the vertical hydraulic gradient = -Δh/ΔL_v and is input as a negative gradient when used with Darcy’s Law (dimensionless)

The sign of the VHG is used to indicate if groundwater is flowing into the pond (positive) or pond water is flowing into the groundwater (negative).

a) The vertical hydraulic conductivity of the bed sediments for A is computed as

K_v = –q/VHG = -15.6 m³/(m²d)/-0.08 = 195.0 m/d

b) The corresponding VHG for B is

VHG = q/K_v = 23.2 m³/(m²d)/136 m/d = 0.17 m/m

Given that no field measurements of head difference are provided, the VHG is positive based on other data given for B. The seepage meter flux is positive so an upward VHG (positive) must be occurring.

The seepage flux for C is

q = –K_vVHG = -155 m/d (-0.05) = 7.8 m³/(m²d)

Once again, the VHG is input as a negative hydraulic gradient and the flux, q, is positive. The flux at this location is upward from the groundwater to the pond.

Return to Exercise 3

License