Box 1 Justification of Terzaghi’s Principle
To justify Equation 3, namely that Σ Ai << 1, we can provide the following rough calculation. Assume the solid grains are spherical with radius r. According to Hertz’s theory (Hertz, 1881), the contact area A’ of two spheres pressed by the force P reads:
| (Box 1-1) |
with Er the sphere Young modulus (which reflects the stiffness of a solid as the ratio of its tensile stress and axial strain, ML-1T-2). Let’s take a representative porous medium depth (250 m) and spheres radius equal to, r = 0.5 mm, and assume full saturation. Considering the buoyant force exerted by water the weight P of a grain column of height h is:
| (Box 1-2) |
where:
| γ′ | = | specific weight of the spheres minus the upward buoyant force (ML−2T−2) |
Using Equation Box 1‑2, A′ above becomes Equation Box 1‑3:
| (Box 1-3) |
Setting h = 250 m, γ′ = 1.7×104 N/m3 (N is a Newton, the SI unit of force [MLT-2], and 1 N is equal to 1 kg m s-2) and Er = 1×1011 N/m2 (corresponding to a volumetric grain compressibility cb,r = 0.16×10‑10 m2/N and a grain Poisson ratio vr = 0.25, being:
![]()
we obtain:
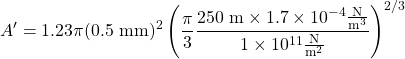
![]()
that is, equal to 0.121 percent of the horizontal projection area of the spheres (equal to 1 mm2). Hence the assumption that Σ Ai << 1 is fully warranted.
