Exercise 2 Solution

Giuseppe Gambolati; Pietro Teatini

Exercise 2 Solution

Question 1: land subsidence after 1 month

Because of the small hydraulic conductivity, it can reasonably be assumed that pressure depletion has not yet significantly propagated into the aquitard. Therefore, similarly to Equation 13, the total subsidence η_tot is the sum of compaction of the phreatic aquifer and the confined aquifer only: η_tot = η_p + η_c.

The compaction of the phreatic aquifer amounts to η_p ≅ t_p c_b_,_p Δσ_z,p with t_p the time‑averaged aquifer thickness below the water table (Equation 10). Denoting the porosity with ϕ and the water saturation with θ_w_, the effective stress change is given by Equation 7.

∆σ_z,p = γ_w ∆z_p (1 − ϕ + θ_w) = 1000 kg/m³ 5 m (1 − 0.35 + 0.10)

= 1000 kg/m³ 3.75 m = $3570\ \textup{kg}/\textup{m}^{2}\ \frac{9.8067\times 10^{-5}\textup{bar}}{\textup{kg}/\textup{m}^{2}}$ = 0.37 bar

Therefore:

η_p = t_p c_b,p ∆σ_z,p = $\frac{1}{2}(25+20)\textup{m}\frac{1\times 10^{-4}}{\textup{bar}}0.37\textup{bar}$ = 0.00083 m = 0.83 mm.

The compaction of the confined aquifer amounts to:

$\\eta _{c}=b_{c}\ c_{b,c}\ \gamma _{w}\ \left ( \Delta z_{c}-\Delta z_{p}(\phi -\theta _{w}) \right )$

$\displaystyle \eta _{c}=50\ \textup{m}\frac{2\times 10^{-5}}{\textup{bar}} \left ( \left ( 1000\frac{\textup{kg}}{\textup{m}^{3}}\left ( 25\ \textup{m}-5\ \textup{m}(0.35-0.1) \right ) \right )\frac{9.8067\times 10^{-5}\textup{bar}}{\frac{\textup{kg}}{\textup{m}^{2}}} \right )$

$\displaystyle \eta _{c}=50\ \textup{m}\frac{2\times 10^{-5}}{\textup{bar}} \left ( 1000\frac{\textup{kg}}{\textup{m}^{3}}\left ( 23.75\ \textup{m} \right ) \frac{9.8067\times 10^{-5}\textup{bar}}{\frac{\textup{kg}}{\textup{m}^{2}}} \right )$

$\displaystyle \eta _{c}=50\ \textup{m}\frac{2\times 10^{-5}}{\textup{bar}}(2.33\ \textup{bar})$

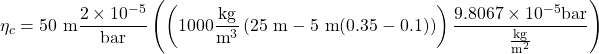
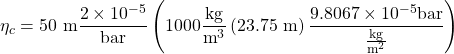
η_c = 0.00233 m = 2.33 mm

Hence: η_tot = 0.83 + 2.33 = 3.16 mm

Question 2: land subsidence after 10 years

In this case, aquitard compaction contributes to land subsidence η_tot = η_p + η_aqt + η_c. After a period of 10 years, it can be assumed that the pressure within the aquitard has reached an equilibrated distribution, with the ultimate aquitard compaction equal to (Equation 28):

$\eta _{aqt}=\frac{1}{2}(\Delta \sigma _{z,p}+\Delta \sigma _{z,c})t_{aqt}c_{b,aqt}$ $= 0.5(0.37\ \textup{bar+2.33\ \textup{bar}})\ 20\ \textup{m}\frac{1\times 10^{-3}}{\textup{bar}}$ = 0.027 m = 27 mm

The cumulative land subsidence is: η_tot = 0.83 + 27.0 + 2.33 = 30.16 mm.

Return to Exercise 2

License